|
نویسنده : www.BartarFile.ir
|
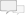
|
حل معادلات دیفرانسیل حاكم بر رفتار یك سیستم از مهمترین مسائلی است كه همواره در زمینه های علوم و مهندسی مورد بحث قرار می گیرد. از آنجایی كه تنها موارد معدودی از این معادلات را می توان مستقیما با روش های تحلیلی حل نمود، روش های عددی زیادی در چند دهه اخیر برای حل چنین معادلاتی پیشنهاد شده است. روش های عددی با ظهور كامپیوترها رشد چشمگیری داشته اند و امروزه به كمك كامپیوترها و این روش ها قادر به حل معادلات بسیار پیچیده در حوزه های متنوع علوم می باشیم. برخی از روش های عددی معروف عبارتند از روش تفاضل محدود، روش اجزای محدود، روش نقاط محدود و روش های جدیدتر مانند روش های بدون مش كه این روش ها هر یك در پی دیگری آمده و به دنبال ایجاد كارایی، دقت، سرعت بالاتر و ایجاد امكاناتی جدیدتر برای حل مسائل و رفع مشكلات روش های قبلی بوده اند. از پركاربردترین این روش ها، روش اجزاء محدود می باشد كه روشی عددی برای یافتن حل تقریبی بسیاری از مسائل مهندسی است. هر چند این روش برای اولین بار جهت تحلیل تنش در سازه هواپیما به كار گرفته شد، لیكن كاربرد آن در بسیاری از مسائل مكانیك جامدات، مكانیك سیالات و علوم به سرعت رو به گسترش نهاد. در زمینه مهندسی راه و ساختمان نیز این روش تحلیل سازه های بسیار پیچیده و طرح بهینه آنها را به طور موثر و اقتصادی ممكن می سازد...
انگیزه انجام نخستین فعالیت ها در زمینه تحلیل هم هندسی (Isogeometric Analysis) ناشی از شکاف موجود بین دنیای تحلیل اجزاء محدود و مدلسازی کامپیوتری بوده است. در مراحل ابتدایی، یکی از مهمترین زمینه های تحقیق در تحلیل هم هندسی ایجاد ارتباط بین دو دسته طراحی و تحلیل، و همچنین مشخص سازی موانع و راه حل های ارائه شده موجود در هر دسته بوده است. مسلما یکپارچه سازی تحلیل و هندسه یک مسئله دشوار است و به نظر می رسد که بایستی تغییرات اساسی برای یکپارچگی کامل طراحی مهندسی و فرایندهای آنالیز انجام شود. روش تحلیل هم هندسی در سال ۲۰۰۵ توسط پروفسور هیوز و همکارانش برای رفع نقص های بیان شده، معرفی شد. توابع هندسی محاسباتی زیادی وجود داشتند که می توانستند به عنوان توابع پایه در تحلیل هم هندسی بکار روند. انتخاب بی اسپلاین (B-Spline) و نربز (NURBS) به عنوان پایه اولیه به دلیل پر کاربرد بودن این توابع هندسه محاسباتی در طراحی مهندسی می باشد...
جزوه آموزش تحلیل مسائل تنش و كرنش صفحه ای بر اساس روش هم هندسی مبتنی بر تئوری اجزاء محدود، ضمن معرفی روش تحلیل هم هندسی و بیان ویژگی های توابع بی اسپلاین و نربز به عنوان اجزاء اصلی آن، روابط مربوط به تحلیل هم هندسی مسائل تنش و کرنش صفحه ای ارائه شده است. ویژگی بارز این گزارش حل مثالی نمونه بر اساس روابط ارائه شده و چهارچوبی که پیش از این در حل مسائل اجزاء محدود مورد استفاده قرار گرفته بود، می باشد. این جزوه مشتمل بر 4 فصل، 50 صفحه، با فرمت pdf، به زبان فارسی، همراه با ذکر نکات، فرمول های مهم و کاربردی، به ترتیب زیر گردآوری شده است:
فصل 1: مقدمه ای بر تحلیل هم هندسی
- مقدمه
- مفهوم تحلیل هم هندسی
- مقدمه ای بر تحلیل هم هندسی بر پایه توابع نربز
فصل 2: معرفی و بررسی توابع بی اسپلاین و نربز
- مقدمه
- نمایش منحنی ها و سطوح
- بی اسپلاین
- بردارهای گرهی
- توابع پایه
- مشتقات توابع پایه بی اسپلاین
- منحنی های بی اسپلاین
- سطوح بی اسپلاین
- نربز
- توابع پایه نربز
- مشتقات توابع پایه نربز
فصل 3: تحلیل هم هندسی در مسائل تنش و كرنش صفحه ای
- تحلیل هم هندسی در مسائل تنش و كرنش صفحه ای
- روابط تحلیل هم هندسی در مسائل تنش و كرنش صفحه ای
- انتگرال گیری عددی
- اعمال شرایط مرزی
فصل 4: حل مثال عددی
- مثال عددی: صفحه مستطیل شكل تحت اثر نیروی برشی
- مراجع
جهت دانلود جزوه آموزش تحلیل مسائل تنش و كرنش صفحه ای بر اساس روش هم هندسی مبتنی بر تئوری اجزاء محدود بر لینک زیر کلیک نمایید:
جزوه آموزش تحلیل مسائل تنش و كرنش صفحه ای بر اساس روش هم هندسی مبتنی بر تئوری اجزاء محدود
نظرات شما عزیزان:
:: موضوعات مرتبط: کتاب و جزوات متلب MATLAB، کلیه گرایش ها، ،



 آمار
وبلاگ:
آمار
وبلاگ: